CC2018-eartsup

Introduction aux Formes et Dessins via p5js

Pour ce cours nous utiliserons la librairie p5js de la fondation processing.

Pour son chargement au sein de votre page HTML référez-vous au cours d’introduction à Javascript

P5JS

P5JS une librairie javascript créée par Lauren McCarthy et développée par la Fondation Processing.

Cette librairie a pour objectif de fournir un modèle simple à tous designer, artiste ou développeur en se basant sur les paradigmes déjà établis par processing et proposer un environnement simple dessin. Ainsi nous y retrouverons de nombreuses méthodes proches du framework Java précédemment utilisé.

setup() & draw()

La plupart des programmes se reposent sur l’utilisation de deux fonctions principales :

Ces deux fonctions sont les composantes de notre programme. Nous aurons donc :

function steup(){
	//initialisation
}

function draw(){
	//boucle principale
}

Canvas

P5js est un librairie permettant de réaliser des dessin et animation interactive sur une page web. Pour ce faire elle créer et utilise une surface permettant de dessiner des formes vectorielles au sein d’un page web : le canvas. L’élément <canvas></canvas> est une balise html permettant la création de surface de dessins 2D ou 3D lorsque celle-ci est définie comme un élément WebGL.

P5js permet de créé automatiquement cette surface sans avoir à intervenir sur le html de notre page par le biais de la fonction createCanvas(largeur, hauteur). Cette fonction créera et ajoutera à la page html l’élément <canvas> à la taille souhaitée.

La référence p5js précise l’élément suivant :

Syntax : createCanvas(w,h,[renderer]) Parameters :

Ici la taille (largeur et hauteur) est définie en pixel. Le renderer correspond quant à lui au moteur de rendu. Ce dernier, optionnel, permet de définir si l’on souhaite travailler dans un contexte 2D P2D ou 3D WEBGL. Ce paramètre est optionnel, s’il n’est pas rempli le contexte sera défini comme un contexte 2D.

Parce que la création du canvas est un élément que nous devons réaliser qu’une seule fois et au départ du programme nous apperlons cette fonction dans la fonction d’initialisation de notre programme soit :

function setup(){
	createCanvas(720, 405);
}

Créer un canvas de la taille de la page

P5js permet également de créer rapidement une surface de dessin de la taille de la page par l’utilisation de deux variables windowWidth et windowHeight. Ces deux variables permettent de récupérer automatiquement la largeur et hauteur de la page. Elle correspond à aux variables window.innerWidth et window.innerHeight en javascript.

Aussi pour créer une surface de la taille de notre prage nous écrirons :

function setup(){
	createCanvas(windowWidth, windowHeight);
}

Changer la taille de la surface de dessin au resize

Parce que chaque personne dispose d’une résolution d’écran différente il est souvent necessaire d’adapter la taille du contenu de sa page web à la résolution disponible pour l’utlisateur. Afin de rendre rendre la surface de dessin responsive en fonction de la taille de la fenêtre nous pourront utiliser la fonction resizeCanvas(largeur, hauteur). Cette dernière permettre de changer la taille du canvas selon une largeur et hauteur fournies.

Si nous souhaitons adpater la taille de notre canvas à celle de la fan^tre de notre navigateur lorsque ce dernier change nous pourrons appeler cette fonction au sein de la fonction windowResized(). Cette dernière est appelée à chaque fois que la fênêtre du navigateur change de taille. Ainsi nous écrirons :

function windowResized(){
	resizeCanvas(windowWidth, windowHeight);
}

Positionner la surface de dessin dans la page

Lorsque que l’on créer une surface de dessin via p5js on remarque que cette dernière est automatiquement ajoutée à la fin de page HTML. En effet dans notre code html nous aurons :

<div class="container">
	<header></header>
	<div class="content"></div>
	<footer></footer>
</div>
<canvas></canvas>

Il est possible, lorsque l’on créer le canvas, de la positionner dans la page au sein d’une ici. Si on reprend la structure ci-dessus, il serait logique d’ajouter notre surface de dessin à la div content. Pour ce faire nous devons, à la création de notre canvas, l’enregistrer dans une variable afin de définir, par la suite, sa div parent par la fonction suivante element.parent('className'). Ainsi nous écrirons :

function setup(){
	var canvas = createCanvas(720, 405);
	canvas.parent('content');
}

Les formes primitives

P5js dispose de différente formes prmitive permettant de dessiner rapidement certaines formes. Vous povez retrouver l’ensemble de ces formes sur la référence de la librairie. Parmis celle-ci on comptera :

Ces fonction étant des fonction des dessins nous les appelerons à l’interieur de la fonction draw() de la manière suivante :

function draw(){
	ellipse(10, 10, 100, 100);
}

RectMode(mode) ellipseMode(mode) : le point d’ancrage

Par défaut le point d’ancrage de la forme primitive rect(x, y, w, h) est le coin haut gauche de la forme alors que celui de ellipse(x, y, w, h) est le centre de l’ellipse. Il est possible de changer la position de ces points d’ancrages par l’utilisation des fonctions rectMode(mode) et ellipseMode(mode). Le paramètre peut être :

Ces fonction s’utilisent de la manière suivante :

rectMode(CENTER);
rect(width/2 - 100, height/2, 100, 100);

ellipseMode(CENTER);
ellipse(width/2 + 100, height/2, 100, 100);

Background, couleur de remplissage et contour

Background

Il est possible de définir la couleur de fond du canvas par l’utilisation de la fonction background(r, g, b). Cette fonction permettant de remplir la surface de dessin d’une couleur elle sera appelée en première dans la fonction draw() soit :

function draw(){
	background(20, 20, 20);
	ellipse(10, 10, 100, 100);
}

Il est important de noter que sans couleur de fond, le programme dessinera en sur-impression, c’est à dire que les dessins effectués aux frames précédentes seront toujours visible en dessous du nouveau dessin. Cela reviendrait, dans Photoshop, à dessiner sur plusieurs claques superposés. La fonction background() a donc pour rôle «d’effacer» les dessins effectués aux frames précédentes.

Lorsque je dessine, à chaque frame, un cercle à la position de ma souris sans utiliser la fonction background() je remarque que les dessins se superposent au fil du temps. Lorsque je dessine, à chaque frame, un cercle à la position de ma souris sans utiliser la fonction background() je remarque que les dessins se superposent au fil du temps.

Si pour ce même code j’utilise la fonction background(), alors je dessinerai un fond entre chaque frame. Les dessins des frames précédentes seront effacés et je verrai alors mon cercle se déplacer. Si pour ce même code j’utilise la fonction background(), alors je dessinerai un fond entre chaque frame. Les dessins des frames précédentes seront effacés et je verrai alors mon cercle se déplacer.

Couleurs de remplissage et de contour

Afin de définir les couleurs de remplissage et de contour d’une forme une utiliserons respectivement les fonction fill(r, g, b) et stroke(r, g, b). La première permettra de définir la couleur du remplissage de la forme alors que la seconde définira la couleur de contour.

parce que notre programme est lu de haut en bas par notre ordinateur, les couleurs de remplissage et de contours doivent être définies avant le dessins de la forme. Ainsi nous aurons :

fill(127, 127, 127);
stroke(0, 0, 127);
ellipse(10, 10, 100, 100);

De même, si nous ne redefinissons pas les couleurs avant le dessin d’une forme, celle-ci prendra les couleurs précédemment définies. L’exemple suivant présente deux ellipses de la même couleur :

fill(127, 127, 127);
stroke(0, 0, 127);
ellipse(10, 10, 100, 100);
ellipse(20, 10, 100, 100)

Dessiner sans contour ou sans ramplissage

Il est également possible de déssiner des formes sans remplissage ou sans contour. Pour se faire nous utiliserons respectivement les deux fonctions noFill() et noStroke() à la place des fonctions fill(r, g, b) et stroke(r, g, b). L’exemple suivante présente une ellipse sans contour et un rectangle sans remplissage :

noStroke();
fill(0, 0, 0);
ellipse(10, 10, 100, 100);

stroke(0, 0, 0);
noFill()
rect(20, 10, 100, 100)

Format des couleurs

Nous aurons noté que l’utilisation des couleurs s’effectue au format R, G, B. il est également possible d’appeler les couleurs au format hexadécimal. Ainsi nous pourrons écrire fill(#40A497). Cela sera identique à fill(64, 164, 151)

Il est également possible d’utiliser un unique paramètre comme valeur RGB afin de définir une valeur de gris. Ainsi lorsque j’écris fill(20), cela revient à écrire fill(20, 20, 20) soit une valeur de gris.

Enfin il est possible d’ajouter un quatrième paramètre aux couleur. Ce dernier correspondra à la couche alpha de la couleur et sera définie entre 0 et 255 comme toute valeur RGB. Ainsi fill(0, 0, 255, 127) permettra de définir une couleur de remplissage bleu avec un aplha de 50%

Transformations et rotations

Lorsque nous dessinons sur nos écrans, nous travaillons sur une grille, une matrice. Dans le cas d’une réalisation de maquette pour un site web, nous travaillons, par exemple, sur des .psd de 12801024 soit une grille de pixels de 12801024, c’est notre matrice. Nous plaçons ensuite nos éléments sur cette grille. Il en est de même avec nos programmes où notre grille commence au point d’origine 0, 0 pour finir au point width, height. Nous allons voir comment manipuler cette matrice.

Matrice du programme

Par défaut le point d’origine (0, 0) de notre matrice se trouve au coin supérieur gauche de notre programme mais il peut être facilement déplaçable.

Déplacer une matrice signifie que l’on décale son point d’origine à un autre endroit. Cela nous donne un autre point de vue et change notre système de géométrie.

Il peut être pratique de déplacer son point d’origine au centre du programme, notamment lorsque nous souhaitons réaliser un programme en symétrie. Ainsi dans le cas d’un rectangle de position 10, 10 dans une symétrie axiale, dont le point d’origine sera le centre de notre programme, le second rectangle aura une position de -10, 10 soit l’inverse de la position x du premier rectangle.

Coordonnées déplacées à width/2 height/2

Afin d’effectuer un déplacement de matrice, nous utilisons la function translate(x, y);. Cela aura pour effet de déplacer la matrice de x pixels en latéral et y pixels en vertical. Le point d’origine 0,0 sera alors en x, y. Il est important de savoir que cette méthode est cumulative, c’est à dire que si nous effectuons, tout au long de notre code, les méthodes suivante :

translate(10, 10);
//code
translate(10, 10);
//code
translate(10, 10)
//code

Cela aura pour effet de déplacer une première fois notre matrice en 10,10 puis en 20, 20 puis en 30, 30. Nous devrons donc effectuer un déplacement inverse si nous souhaitons positionner la matrice à son premier point d’origine.

Déplacement de matrice cumulatif

Afin d’éviter de nombreuses transformations retour durant notre code, il est possible d’isoler notre déplacement de matrice à l’aide des méthodes suivante :

push();
translate(10, 10);
//code
pop();

push() permet à un instant T d’enregistrer les coordonnées du point d’origine afin de pouvoir les restituer à l’aide de la commande pop()

À l’exécution de ce code, la matrice se déplacera en position x, y lors de la fonction translate(), puis reviendra à son point d’origine lors de la fonction pop(). Cela nous permet donc de changer notre géométrie à un instant T et de dessiner l’ensemble de nos formes voulues dans ce nouveau système de géométrie encadrée par les méthodes push() et pop()

push()/pop()

La rotation d’un élément est un cas particulier. Pour bien comprendre son fonctionnement revenons au point de vue microscopique de notre espace de travail, le pixel.

Nous souhaitons dessiner un rectangle de position 10, 10 et de taille 10, 10.Puis nous souhaitons effectuer un rotation de 45° de ce même rectangle. Le pixel est un élément dessiné, 0 ou 1, plein ou vide, il ne peut être rempli de manière partielle. Lorsque nous effectuons ce genre de manipulation dans photoshop, notre logiciel dessine notre diagonale sous forme de pixels pleins ou vides.

Rotation de matrice

Cette transformation utilisée par photoshop n’est pas la plus simple à réaliser et processing utilise un autre méthode.

Au lieu de redessiner les pixels de notre rectangle, nous allons effectuer une rotation de notre espace de coordonnées à l’aide la fonction suivante rotate(angle). Nous noterons que p5js définit ses angles en radians. Cette méthode permet donc faire faire une rotation à notre matrice et ce depuis son point d’origine.

Rotation de matrice

Pour obtenir notre rectangle à une véritable position 10, 10 et ayant effectué une rotation à 45° nous devons donc déplacer la matrice un premier temps, puis effectuer la rotation.

Rotation de matrice

Pour ce faire nous utilserons la méthode suivante :

push();
translate(10, 10);
rotate(degrees(45));
pop();

Formes personnalisées

Si les formes primitives permettent de résaliser de nombreux dessins il y a de nombreux cas dans lesquels il est necessaire de dessiner des formes personnalisé tel que dans l’exemple ci-dessous.

exemple de forme personnalisée

Il est possible de dessiner ces formes avec p5js à l’aide des fonctions beginShape([MODE]), vertex(x, y) et endShape([MODE]). Ces trois fonctions permettent permettent de dessiner une forme personnalisée où chaque chaque sommet sera décris par la fonction vertex(x, y)

La fonction beginShape([MODE]) permet de définir et ouvrir le dessins de la forme, la fonction vertex(x, y) permet de décrire les sommets et la fonction endShape([MODE]) permet, quant à elle, de finir la forme. Elles s’utilisent de la manière suivante :

beginShape();
vertex(0, 0);
vertex(40, 0);
vertex(40, 40);
vertex(0, 40);
endShape();

Les fonctions beginShape([MODE]) et endShape([MODE]) peuvent également prendre un paramètre optionnel permettant de définir la manière dont la forme sera dessiné (Points, lignes, quadrilateres, quadrilateres reliés, triangle, triangles reliés, triangle fan et forme fermée)

Shape types

Formes procédurales et coordonnées polaires

Les formes personnalisée necessitant la description de chaque sommet les composants elle sont souvent générée de manière procédurale. Dans l’exemple suivant nous réaliserons une forme procédurale dont chaque point reparti de manière uniforme sur un cercle de coordonnée identique mais dont le rayon diffère de manière aléatoire.

Procedural Shape

Pour ce faire nous aurons besoins de éléments suivant :

Afin de répartir les point de manière uniforme nous allons utiliser le système de coordonnées polaires. En géométrie un espace polaire est un espace géométrique à deux dimensions dans lequel les coordonnées d’un point sont définie par une valeur d’angle et une distance (rayon).

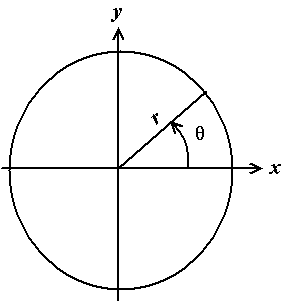
polar coordinates

Ce système de coordonnées et particulière pratique dans la création de systèmes circulaires tels que les pendules, spirales ou autre. Pour réaliser un système polaire il est nécessaire de connaître l’équation nous permettant de positionner un point sur un cercle à partir d’un angle et d’une distance. Avant d’aller plus loin dans le dessin de notre forme et pour mieux comprendre le système de coordonnées polaires il est necessaire de faire un retour sur le rapport trigonométrique

Le rapport trigonométrique

La trigonométrie traite des relations entre distances et angles dans les triangles et notamment dans le triangle rectangle. C’est ce dernier qui va nous intéresser plus particulièrement.

Faisons un rapide bon dans le passé concernant ce triangle. Un triangle rectangle se caractérise par un angle droit (90°) et la somme de ses angles est égale à 180°. L’angle droit est donc son angle le plus grand. Enfin le côté opposé à cet angle s’appel l’hypoténuse et se caractérise par le fait qu’il est le côté le plus grand de ce triangle.

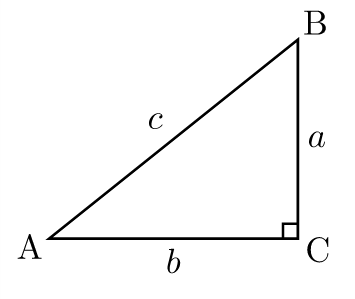
Triangle Rectangle

Si on s’intéresse à l’angle BAC et aux fonctions trigonométriques alors nous remarquons que :

sin(BAC) = a/c cos(BAC) = b/c tan(BAC) = a/b

Nous avons ici les fonctions auxquelles nous allons prêter attention. Allons maintenant plus loin en traçant un cercle dont l’origine sera A et de rayon AB (notre hypothénuse). Partons du principe que notre hypoténuse AB a une valeur de 1. Nous obtenons alors un cercle trigonométrique.

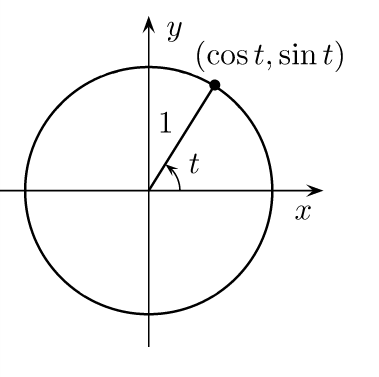
Polar coordinates

Si on observe ce cercle nous remarquons que les coordonnées du point B peuvent être définies de la sorte :

x = cos(t) y = sin(t)

Or nous savons ici que notre hypothénuse à un valeur de 1. Si nous voulons être correcte dans nos cordonnées, nous obtenons :

x = cos(t) × 1 y = sin(t) × 1

Nous venons de voir la formule permettant de calculer les coordonnées d’un point sur un cercle. Nous avons ici l’une des formules que nous utiliserons le plus dans nos programmes par la suite.

x = cos(angle) × rayon y = sin(angle) × rayon

Nous venons de voir à quoi les fonctions trigonométriques Sinus et Cosinus pouvaient nous être utile, attardons nous maintenant sur la dernière, la Tangente. La tangente est le rapport du sinus au cosinus, par définition :

tan(angle) = sin(angle)/cos(angle)

On appelle tangente de l’angle aigu , le nombre noté tan(angle) défini par BC/AC. Nous savons aussi que la tangente d’un angle est égale au côté opposé / côté adjacent ou dans notre cas à b/a. Pour obtenir notre angle il nous faudra alors obtenir l’inverse de cette tangente. Ainsi l’angle BAC sera égale à :

angle = atan2(a, b)

triangle Rect

Retour à la forme

Nous avons vu plus haut que les coordonnées d’un point sur un cercle sont définies par :

x = cos(angle) × rayon y = sin(angle) × rayon

Nous pouvons donc préciser l’algorithme de notre forme de la manière suivante :

Nous traduirons ça dans notre programme de la manière suivante :

//definition du nombre de points et de l'origine de la forme
var nbPoints = 100;
var origineX = width/2;
var origineY = height/2;

//ouverture de la forme
beginShape()
//pour chaque point
for(var i=0; i<nbPoints; i++){
	//Répartir l'angle du point i de manière uniforme sur 360°
	var angle = i * (TWO_PI / nbPoints);
	//Définir un rayon aléatoire pour le point i
	var rayon = random(100, 200);
	//Définir les coordonées x, y du point i
	var x = cos(angle) * rayon + origineX;
	var y = sin(angle) * rayon + origineY;
	//dessiner le sommet i
	vertex(x, y);
}
//fermer la forme
endShape(CLOSE);

Nous remarquons ici l’utilisation de la méthode random(100, 200) Cette méthode propre à p5js permet de retourner un nombre aléatoire entre deux valeur x et y.

interaction clavier/souris

P5js permet également d’accéder à des fonction d’interaction tel que le clique souris ou les l’appuie sur une touche du clavier.

Interaction souris

Pour définir une interaction souris sur la page de notre programme nous pourrons utiliser les fonctions suivante :

Elles s’utilisent en dehors de la fonction draw() de la manière suivante :

function mousePressed(){
	//la souris à été cliqué
}

Il est également possible de savoir lorsque qu’un évènement souris se produit au sein de la fonction draw(). Pour se faire nous pouvons accéder aux valeur variables suivantes :

Interaction clavier

Pour définir une interaction souris sur la page de notre programme nous pourrons utiliser les fonctions suivante :

Comme pour les fonctions souris ces fonctions s’utilisent en dehors de la fonction draw() de la manière suivante :

function keyPressed(){
	//un touche du clavier est appuyé
}

Il est possible de connaitre la touche appuyé au sein de ces fonction par l’utilisation des variables suivantes :

Elles s’utilisent de la manière suivante :

function keyPressed(){
	if(key == 'a'){
		//a est la dernier caractère appuyé
	}
	if(keyCode == UP_ARROW){
		// la touche flech haute a été appuyé
	}
}

Il est également possible de savoir lorsque qu’un évènement clavier se produit au sein de la fonction draw(). Pour se faire nous pouvons accéder aux variables/fonctions suivantes :

Elle s’utilisent de la manière suivante :

function draw(){
	if(keyIsDown(UP_ARROW)){
		// la touche flech haute estappuyée
	}

	if(keyIsPressed == true){
		//une touche est appuyée
	}
}

Variables p5js

P5js permet également d’accéder à différentes variables telle que :

Exemples :

This site is open source. Improve this page.