CC2018-eartsup

Grilles, récursions et aléatoires

Grilles cartésiennes

La grille est l’un des éléments principaux du design graphique, on la retrouve dans de nombreux domaines tel que :

En design graphique la grille est une structure (souvent en 2 dimensions) réalisée par partir d’un série d’intersection entre des éléments (généralement des ligne horizontale et vertical). Pour en savoir plus sur la grille de mise en page je vous invite à vous rendre sur le site de l’atelier Nun :

La grille de mise en page a été théorisée par le graphiste suisse Joseph Muller Brockmann dans les année 1960, notamment dans son ouvrage Grid Systems in Graphic Design. Elle permet de découper le format dans sa largeur (et plus tard dans sa hauteur) en plusieurs parties égales, séparées par des espaces verticaux. L’usage des colonnes ainsi créées permet de travailler avec des « zones », proportionnelles entre elles, ce que l’œil du lecteur perçoit immédiatement.

Dans le cas d’un motif ou d’un frise, la grille permet de définir la structure en 1, 2 ou 3 dimensions de répétition d’une forme (1 dimension pour la frise et 2 pour le motif). On retrouve l’utilisation de ces motifs dans de nombreux travaux graphiques tel que :

Grille cartésienne

En géométrie, rappelons qu’un espace cartésien est un espace géométrique permettant de définir la position d’un point dans un espace munie d’un repère cartésien définie par droite x, y et z (horizontal, vertical, et en profondeur)

Espace cartésien

Afin de réaliser notre motif nous allons utiliser ce système de grille afin de définir les coordonnées de notre motif à répéter sur les axe x et y.

Pour cette exercice nous utiliserons un motif simple, le rectangle.

Rect

Cette forme est définie par les variables suivantes :

La frise

Dans un premier temps nous allons réaliser une frise. Une frise est un répétition, sur un axe, d’un motif. Dans notre cas nous réaliserons notre frise sur l’axe X.

frise

La frise étant composé d’une répétition de motif nous pouvons la réaliser en utilisant un structure itérative. En effet ces structure nous permettent de réaliser une répétition d’action (ici le dessin d’un rectangle). Si nous regardons notre frise de prêt nous pouvons la décomposer de la sorte

Nous traduirons cela dans p5js de la manière suivante :

var x = 0;
var y = height/2;
var largeur = 50;
for (var i=0; i<5; i++) {
    var newX = x + i * largeur;
    rect(newX, y, largeur, largeur);
}

Le modulo

Nous pouvons facilement réaliser une frise à plusieurs motif tel que défini par le modèle suivant :

modulo

Si nous pouvons définir cette frise par les instruction suivantes :

Le problème principale étant de résoudre le problème “Une fois sur deux”; pour ce faire nous utiliserons le modulo (%). Le modulo (%), en programmation, permettant d’obtenir le reste d’une division. Par exemple si la division de 5 par 2 donne le résultat 2, nous aurons un reste de 1. Ainsi le modulo de 5 par 2 nous renverra le résultat 1.

5/2 = 2 avec un reste de 1
5%2 = 1 soit le reste de la division de 5 par 2

Lorsque nous effectuons un modulo sur un suite de nombre E divisée par une certain nombre X nous obtenons un résultat intéressant. En effet le modulo nous renverra une suite de résultat se répétant en fonction du dénominateur (diviseur). Ainsi nous obtenons les résultats suivant :

→ Soit une suite de nombre allant de 0 à 5 en incrémentant de 1
→ Soit un dénominateur X

Si X = 2
  0%2 = 0
  1%1 = 1
  2%2 = 0
  3%2 = 1
  4%2 = 0
  …
Si X = 3
  0%3 = 0
  1%3 = 1
  2%3 = 2
  3%3 = 0
  4%3 = 1
  5%3 = 2
  ...
Si X = 4
  0%4 = 0
  1%4 = 1
  2%4 = 2
  3%4 = 3
  4%4 = 0
  5%4 = 1
  6%4 = 2
  7%4 = 3
  ...

Nous pouvons donc facilement définir notre changement de forme une fois sur deux par l’utilisation d’un modulo de 2 (%2) et d’un condition. En effet il nous suffit de savoir si le modulo de l’itération en cours (défini par i) renvoie un nombre pair (0) ou impaire (0). Dans le premier cas nous dessinerons un rectangle, sinon nous dessinerons une ellipse.

for (var i=1; i<5; i++) {
    var newX = x + i * largeur;
    if (i%2 == 0) {
      ellipseMode(CORNER);
      ellipse(newX, y, largeur, hauteur);
    } else {
      rect(newX, y, largeur, hauteur);
    }
  }

Le pavage

Nous allons maintenant réaliser un pavage. Un pavage est une répétition d’un motif sur plus d’un axe. Il s’agit d’une évolution de la frise. Ici nous réaliserons un pavage sur deux dimensions

Pavage

Lorsque nous observons le pavage nous remarquons qu’il s’agit d’une répétition de la frise que nous avons précédemment réalisé. En d’autre terme nous pourrions dire :

Un pavage est la répétition d’une frise qui est elle même la répétition d’un motif (inception!!!!).

Si un pavage est la répétition d’un répétition nous pouvons donc le définir de la manière suivante :

soit à l’aide de p5js :

for (var i=0; i<3; i++) {
    for (var j=0; j<5; j++) {
      var newX = x + j * largeur;
      var newY = y + i * hauteur;
      rect(newX, newY, largeur, hauteur);
    }
  }

Comme pour la frise, nous pouvons ajouter diverse variations à notre frise tel qu’une marge séparant les formes, une variation de couleur, de tailles…

Grilles polaires

Nous l’avons vu la grille cartésienne est un élément permettant de réaliser des répétition de motif sur les axes XY que ce soit des frises ou des pavages. Cependant il ne s’agit pas du seul système de coordonnées possible. Parmi les différents systèmes de coordonnées il en est un que nous retrouvons régulièrement dans les arts graphique, le VFX ou les jeux vidéo : le système de coordonnées polaires (voir cours d’introduction aux formes et dessins).

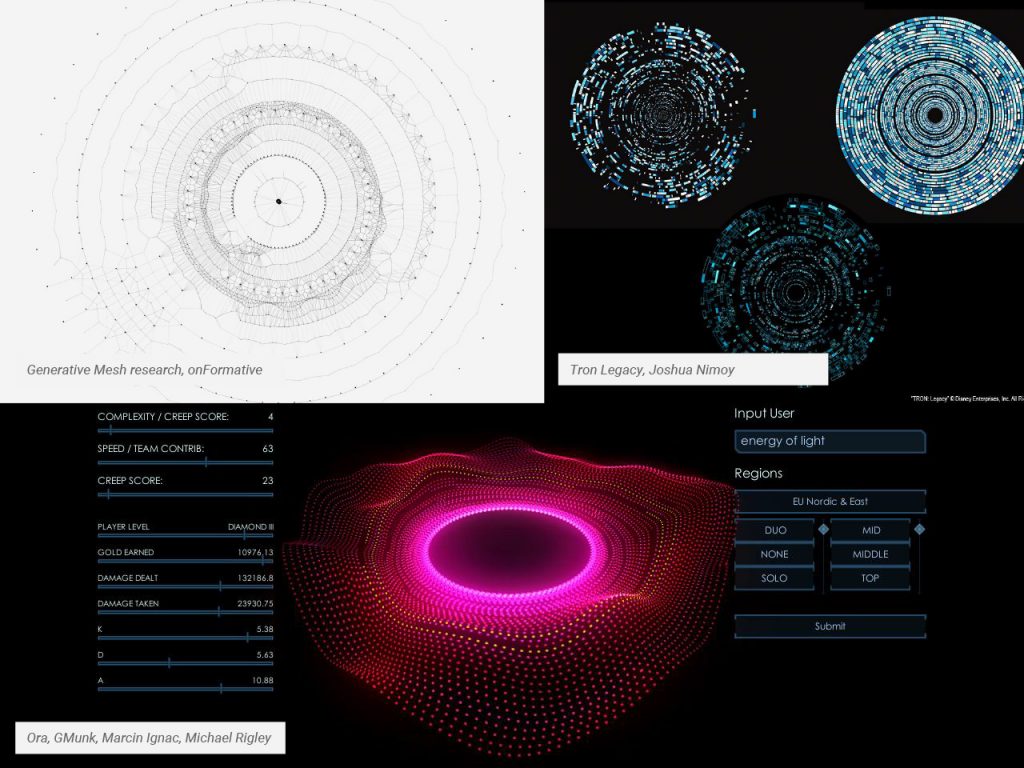
Grilles polaires

Pour rappel, en géométrie un espace polaire est un espace géométrique à deux dimensions dans lequel les coordonnées d’un point sont définie par une valeur d’angle et une distance (rayon). Ce système de coordonnées et particulière pratique dans la création de systèmes circulaires tels que les pendules, spirales ou autre. Pour réaliser un système polaire il est nécessaire de connaître l’équation nous permettant de positionner un point sur un cercle à partir d’un angle et d’une distance.

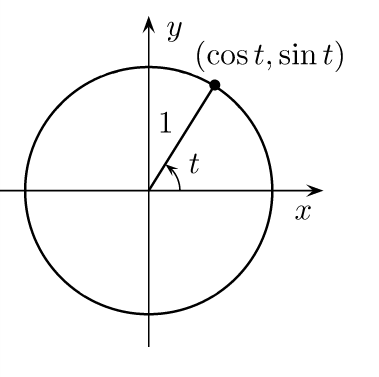
Coordonnées polaires

Une fois que nous connaissons l’équation permettant de placer un point sur un cercle nous pouvons facilement réaliser la frise suivante :

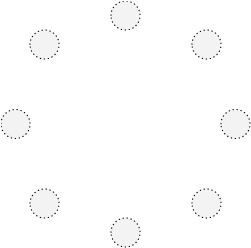
frise polaire

Une frise étant composé d’une répétition de motif nous pouvons la réaliser en utilisant un structure itérative. Nous pouvons définir la frise de la manière suivante :

Ce qui nous donneras avec p5js :

var X = width/2;
var Y = height/2;
var rayon = 100;
for(var i=0; i<8; i++){
  var ni = i / 8; //on normalise i
  var angle = TWO_PI * ni;
  var ex = X + cos(angle) * rayon;
  var ey = Y + sin(angle) * rayon;
  ellipse(ex, ey, largeur, hauteur);
}

Une fois la frise réaliser nous pouvons facilement réaliser une grille polaire (aussi appelé pavage) par l’utilisation d’une répétition de la répétition du motif, soit une double structure itérative :

Grille polaire

Ce qui nous donneras avec p5js :

var X = width/2;
var Y = height/2;
var rayonRef = 100;
for(var i=0; i<2; i++){
  var ni = i / 2; //on normalise i
  var rayon = rayonRef + rayonRef * i;
  for(var j=0; j<8; j++){
    var nj = j / 8; //on normalise j
    var angle = TWO_PI * nj;
    var ex = X + cos(angle) * rayon;
    var ey = Y + sin(angle) * rayon;
    ellipse(ex, ey, largeur, hauteur);
  }
}

Grille polaire uniforme

Si l’exemple ci-dessus nous montre comment réaliser une grille polaire simple on remarque que cette dernière aura rapidement une forme d’étoile. En effet chaque itération de frise ayant le même nombre d’élément, plus le rayon sera grand plus les motifs composant la frise seront espacés, créant ainsi un effet de type étoile.

Pour réaliser une grille polaire davantage uniforme il nous faudra alors changer le nombre de motif composant chaque frise de la grille. Plus rayon de la frise sera grande plus le nombre de motif la composant sera grand. Pour ce faire nous pouvons utilisera la méthode suivante :

Ici on remarque que le nombre de motifs composant la frise est obtenue en divisant le périmètre du cercle par l’espace séparant ces motif. En géométrie, le périmètre d’un cercle est obtenu par le calcul suivant : P = 2 * PI * rayon.

Ainsi, en programmation notre grille sera définie de la manière suivante :

var res = 20.0;
var radius = height /2;
var numberOfInnerCircle = 25;

var ox = width/2;
var oy = height/2;

for(var i=0; i<numberOfInnerCircle; i++){
  var ni = i/numberOfInnerCircle;
  var rad = radius * ni;
  var perimeter = TWO_PI * rad * 2.0;
  var numberOfElement = floor(perimeter / res);

  for(var j=0; j<numberOfElement; j++){
    var theta = (j/numberOfElement) * TWO_PI;
    var x = cos(theta) * rad + ox;
    var y = sin(theta) * rad + oy;
    ellipse(x, y, res * 0.35, res * 0.35);
  }
}

Ce qui nous donnera le motif suivant :

Grille polaire uniforme

La Récursion

Le principe de la récursion est d’effectuer une action en boucle en appelant une function à l’intérieur d’elle même.

Ainsi un exemple de base serait :

void uneFunction(){
 uneFunction();
}

Ce code ne génère aucun résultat, mais la function est effectuée en boucle jusqu’à l’arrêt du programme.

Ainsi en appelant une function à l’intérieur d’elle même nous créerons une boucle qui sera possible d’arrêté à l’aide de condition. L’autre avantage c’est qu’il sera ainsi possible de faire passer des variables pour effectuer des calculs et donc modifier les valeurs à chaque boucle.

function setup(){
  drawCircle(width/2,height/2,200);
}

function drawCircle(x, y, radius) {
  ellipse(x, y, radius, radius);
  if(radius > 2) {
    radius *= 0.75f;
    drawCircle(x, y, radius);
  }
}

Dans cet exemple la function commence par dessiner un cercle, elle regarde ensuite si le rayon est supérieur à 2px , si c’est le cas la valeur dans la variable rayon est modifié et la function est rappelé pour effectuer une nouvelle fois les mêmes opérations.

Il est vrai que nous pourrions effectuer la même opération avec les bouche for ou while mais l’intérêt des récursions vient lorsque nous souhaitons créer des subdivisions presque infinies. Car rien n’empêche la function de s’appeler plus d’une fois à l’intérieur d’elle même. Ainsi une function pourrait lors de son exécution s’appeler 2 fois. Chacune de ces deux fois se rappellerait deux fois ……

Image of Circle

function setup() {
  createCanvas(900, 600);
drawCircle(width/2, height/2, 900);
}

function drawCircle(x, y, radius) {
  noFill();
  ellipse(x, y, radius, radius);
  if(radius > 8) {
    drawCircle(x + radius/2, y, radius/2);
    drawCircle(x - radius/2, y, radius/2);
    drawCircle(x, y + radius/2, radius/2);
    drawCircle(x, y - radius/2, radius/2);
  }
}

Dans cet exemple la function est appelée une première fois puis s’appelle quatre fois, chaque appel rappelle 4 fois, etc etc jusqu’a que la condition n’est plus respectée. À chaque nouvel appel de la function les variables de tailles et de positions sont modifiées pour créer un pattern géométrique.

Un autre exemple appelé Cantor d’après le nom de sont créateur un mathématicien Allemand.

Image of Cantor

function setup() {
  createCanvas(900, 600);
  cantor(0,0,900);
}
function cantor( x, y, len) {
  if (len >= 1) {
    line(x,y,x+len,y);
    y += 20;
    cantor(x,y,len/3);
    cantor(x+len*2/3,y,len/3);
  }
}

Tree

Un des exemples les plus utilisés pour présenter la récursion est l’arbre. Voici son code : Image of Tree

// Recursive Tree Processing
// Daniel Shiffman <http://www.shiffman.net>

function setup() {
  createCanvas(400, 300);
  background(255);
  // Start the tree from the bottom of the screen
  translate(width/2, height);
  stroke(0);
  branch(60);
}

function draw() {


}

function branch(len) {
  strokeWeight(2);

  line(0, 0, 0, -len);
  // Move to the end of that line
  translate(0, -len);

  len *= 0.66;
  // All recursive functions must have an exit condition!!!!
  // Here, ours is when the length of the branch is 2 pixels or less
  if (len > 2) {
    push();    // Save the current state of transformation (i.e. where are we now)
    rotate(PI/5);   // Rotate by theta
    branch(len);       // Ok, now call myself to draw two new branches!!
    pop();     // Whenever we get back here, we "pop" in order to restore the previous matrix state

    // Repeat the same thing, only branch off to the "left" this time!
    push();
    rotate(-PI/5);
    branch(len);
    pop();
  }
  delay
}

Cet exemple utilise la même technique que ceux précédemment présentés. La différence vient du fait qu’a la place de dessiner l’objet à tel ou tel position nous avons besoin d’utiliser les function de transformation pour faire bouger le plan de travail.

Dans un premier temps la fonction est appelée et vient dessiner la base de l’arbre. Nous allons ensuite déplacer le plan de travail pour que le 0,0 se trouve au bout de la branche précédemment créer. Nous vérifions que la longueur est plus grande que 2px puis nous faisons faire une rotation à notre plan de travail dans un sens avant d’appeler une nouvelle fois la fonction. Pour créer la branche dans l’autre sens nous recommencerons cette action. Nous pouvons remarquer que nous utilisons des push() et pop() pour que les rotations ne soient prises en compte que par les appels de fonction voulus.

L’appel à la fonction branch ce faisant entre push() et pop() ça sera tous les objets dessinés par la fonction qui seront affectés par cette rotation. Ce qui permet de créer les branches de l’arbre.

Maintenant que nous avons créé un arbre symétrique, que se passerait-il si nous rajoutions du random pour que les arbres soient différents.

Image of tree https://codepen.io/rickyeckhardt/pen/Gkpez

Aléatoires browniens et perlin

Nous pouvons facilement ajouter une variation graphique à un visuel par l’utilisation d’une valeur pseudo-aléatoire. En programmation on appel ces valeurs pseudo-aléatoire car elle sont définie par une équation et sont donc prévisible, cependant elles offre une large possibilité de variations. Parmis le différents types d’aléatoires on compte l’aléatoire browniens qui offre des valeurs chaotiques et l’aléatoire perlin qui offre des valeurs plus douces.

Aléatoire brownien

Le bruit brownien est un aléatoire où les valeurs produites sont réparties de manière totalement aléatoire. Chaque valeur pourra être grandement espacée les une des autres ou totalement proche voir identique. Une répartition brownienne peut être imaginé par ce schema :

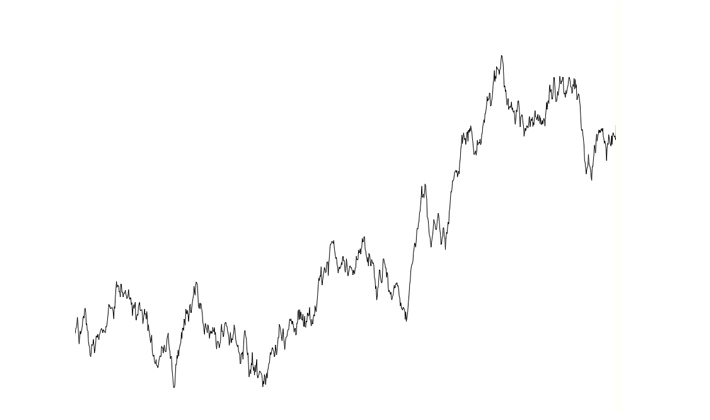
Aléatoire brownien

En javascript il est possible de générer un nombre aléatoire par l’utilisation de la méthode ````Math.random()``` (voir cours d’introduction sur le javascript. Cette dernière permet de retourner un nombre décimal (pseudo) aléatoire compris entre 0 et 1. Nous pourrons alors facilement changer le rang de cette valeur par une simple opération arithmétique. Ainsi pour obtenir une valeur comprise entre 50 et 150 nous écrirons :

var x = 50 + Math.random() * 100;

P5js permet également d’obtenir des valeurs aléatoires sans avoir à réaliser d’opération arithmétique. POur cela nous utiliserons la méthode ````random(v1, v2)```. Cette méthode nous renverra alors un nombre aléatoire compris entre v1 et v2. Ainsi pour obtenir une valeur comprise entre 50 et 150 nous écrirons :

var x = random(50, 150);

Aléatoire perlin

Le bruit perlin est bien différent du bruit brownien tant dans sa syntaxe que dans les valeurs qu’il renvoie. Contrairement au bruit brownien le bruit perlin produit une séquence de valeurs où chaque valeur est proche de la valeur précédente. On obtient donc une répartition harmonieuse de valeurs. Similaire à la notion d’harmoniques en physique, le bruit perlin est calculé sur plusieurs octaves qui sont traitées par lot pour le résultat final. On peut illustrer le bruit perlin par ce schéma :

Bruit perlin

Le bruit de perlin a été développé par Ken Perlin en 1985. À cette époque, après avoir travaillé sur les effets spéciaux de Tron pour MAGI en 1981, il cherchait à éviter le look « machinique ». Il commença donc par mettre au point une fonction pseudo-aléatoire de bruit qui remplit les trois dimensions de l’espace, avant d’inventer l’année suivante le premier langage de shading. Ses travaux sur les textures procédurales ont valu à Ken Perlin l’Academy Award for Technical Achievement en 1997.

Ce bruit est très utilisé dans la génération de textures procédurales mais aussi dans les déplacements de particules puisque nous permet d’avoir une harmonie entre les valeurs et donc des sensations d’incrémentation et décrémentation plus douces. Dans sa syntaxe le bruit perlin est bien différent du bruit brownien. Voici comment il se déclare :

var n = noise(v1); //pour un bruit à 1 dimension
//ou
var n = noise(v1, v2); //pour un bruit à 2 dimensions
//ou
var n = noise(v1, v2, v3); //pour un bruit à 3 dimensions

On remarque de prime abord que là où le bruit brownien accueille deux valeurs entre ses parenthèses (minimum et maximum) le bruit perlin peut en accueillir trois. En effet on dit du bruit perlin qu’il peut être uni, bi ou tridimensionnel. Nous nous attarderons sur le bruit perlin unidimensionnel dans cette partie.

La seconde remarque que nous ferons sur le bruit perlin est qu’il ne nous renverra toujours qu’une seule valeur comprise entre 0 et 1 et celle-ci sera toujours identique. En effet la répartition de bruit perlin est définie par la valeur précédente obtenue. Il faudra donc incrémenter notre valeur puis recalculer notre bruit afin d’obtenir une suite de valeurs réparties de façon harmonieuse.

Pour cela nous allons utiliser une valeur que nous appellerons xInc et qui sera égale à 0. Nous calculerons un bruit à partir de cette valeur puis à la fin de chaque boucle nous l’incrémenterons de 0.01 pour calculer un nouveau bruit à partir de la valeur précédente.

var xInc = 0.0;

function draw(){
  var n = noise(xInc);
  xInc += 0.01;
}

Nous obtenons donc une suite de valeurs harmonieuses dépendante de la valeur précédente. Cependant nos valeurs restent comprises entre 0 et 1. Pour obtenir nos valeurs entre 50 et 150 il faudra donc effectuer une opération arithmétique qui nous renverra nos valeurs sur une échelle de 50 à 150 tel que :

var xInc = 0.0;

function draw(){
  var n = 50 + noise(xInc) * 100;
  xInc += 0.01;
}

Exemples :

This site is open source. Improve this page.